Archimedes

Archimedes









Period : about 287-212 B.C.
Mathematical issues involved :
· Algebra : cubic equation ; numbering system ; linear equations ;
· Physical : hydrostatic , water pump screw ;
· Spatial Geometry : areas of a sphere , a spherical cap , a spherical surface area , volume of a sphere ;
· Plane Geometry : classic method for calculating pi , the quadrature of the parabola ; Archimedean Spiral ; formula of Heron ;
One of the greatest mathematicians of the third century BC , from the city of Syracuse , on the island of Sicily . Was born about the year 287 BC and died during the Second Punic War in 212 BC in Syracuse . He was the son of an astronomer and also acquired a reputation in astronomy .
Archimedes may have studied in Alexandria for some time with the students of Euclid , and maintained communication with mathematicians there, as Conon , Dosite and Eratosthenes .
Legend has it that Syracuse resisted the siege of Rome for nearly three years , due to the ingenious war machines invented by Archimedes to leave your enemies in the distance. Among them : catapults to throw stones, ropes , pulleys and hooks to lift and shatter the Roman ships ; inventions to burn the ships .
The works of Archimedes exhibit great originality , computational skill and accuracy in the statements . There are about ten treaties that have been preserved to this day and there are traces of others.
The treatises on plane geometry are: The measure of a circle where Archimedes inaugurated the classic method for calculating http://www.matematica.br/historia/imagens/arquimedes-001.jpg ; Squaring the parable consists twenty four propositions which shows that the area of a parabolic segment is four thirds of the triangle inscribed same base and vertex at the point where the tangent is parallel to the base area . This involves deducting the sum of a convergent geometric series ; About Spirals composed twenty-eight propositions which are devoted to the properties of the curve ( known today as Archimedes Spiral ) and whose polar equation is http://www.matematica.br/ historia/imagens/arquimedes-002.jpg , in particular, is the area encompassed by the curve radii and two vectors in a manner substantially the same as that of an exercise now be integral calculation area .
Through the Arabs know that the usual formula for the area of a triangle in terms of its sides , known as Heron's formula - where s is the semiperímetro - was known to Archimedes several centuries before Heron was born. Pappus mentions in his works the treaty Archimedean levers About cites and Teon in their jobs a theorem of Archimedes found in the treatise The Theory of Mirrors .
The treatises on spatial geometry are: On the Sphere and Cylinder written in two volumes and consists of fifty-three propositions about, among other things , the theorem that provides areas of a sphere and a spherical cap . Shows that the area of ​​a spherical surface is exactly two -thirds of the total surface area of the right circular cylinder circumscribed to it and the volume of the sphere is exactly two thirds of the volume of the same cylinder . Book II includes the problem of slicing a sphere with a plan in order to obtain two spherical segments whose volumes are given a reason . This problem leads to a cubic equation where a discussion is made concerning the conditions under which the cube can have a positive real root .
Archimedes wrote small works on arithmetic, one of them is The counter of sand, which is a curious question : how to determine the amount of grains of sand can fill a sphere of radius and center on Earth reaching the Sun , ie , the size of the universe . In this work we find comments related to astronomy, where Archimedes used the model of the universe of Aristarchus of Samos , who advanced the heliocentric theory of Copernicus . Archimedes will calculate the amount of sand needed to fill a thimble , a stadium , the volume of the Earth and so on , until it fills the entire universe . Simultaneously and in parallel , will develop a numbering system ( which led to the invention of logarithms ) can express the values ​​found in this calculation . There is also the problem of cattle which involves eight whole seven unknowns related linear equations and still subject to two additional conditions namely that the sum of unknowns right pair of a perfect square and the sum of another pair is given a number of unknowns triangular . No additional conditions , the lowest values ​​of the unknowns are numbers in the millions , with these conditions , one of the unknowns must be a number with more than 206 500 digits !
There are two works of Archimedes on applied mathematics : On the Equilibrium of Plane Figures and On Floating Bodies . The first one consists of two books and contains twenty- five propositions which through a postulacional treatment , we obtain the elementary properties of the centroids and the centroid determine various flat areas , ending with the parabolic segment and a limited area of a parabola and two parallel strings. On Floating Bodies consists of two books ninety propositions , and represents the first application of mathematics to hydrostatic . The treaty is based on two postulates first developing the familiar laws of hydrostatic and then considers some very difficult problems , concluding with a noteworthy study on the resting position and stability of a ( straight) segment of paraboloid of revolution immersed in a fluid .
The treatise The Method is in the form of a letter to Eratosthenes and is important because of the information it provides on the method Archimedes used to discover many of his theorems . Archimedes used it experimentally to find out results that he then tried to put in rigorous terms by the method of exhaustion.
Are attributed to two other jobs lost Archimedes : About Calendar and About Building balls . In the latter there was a description of a planetarium built by him to show the movements of the sun, moon and the five planets known in his time . Probably the mechanism was triggered by water .




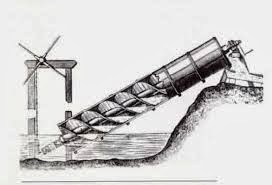
The best known mechanical invention of Archimedes is the water pump screw , he built to irrigate fields , ponds drain and remove bilge water from ships . The mill is still used today in Egypt

Tweet