Arquímedes

Arquímedes









Período : alrededor 287-212 aC
Problemas matemáticos involucrados:
· Álgebra : ecuación cúbica ; sistema de numeración ; ecuaciones lineales ;
· Física : hidrostática , tornillo de la bomba de agua ;
· Geometría del espacio : áreas de una esfera , un tapa esférica , un área de superficie esférica , volumen de la esfera ;
· Geometría plana : método clásico para el cálculo de pi, la cuadratura de la parábola ; Arquímedes Espiral ; fórmula de Heron ;
Uno de los más grandes matemáticos del siglo III aC , de la ciudad de Siracusa, en la isla de Sicilia. Nació hacia el año 287 aC y murió durante la Segunda Guerra Púnica en el 212 aC, en Siracusa . Él era el hijo de un astrónomo y también adquirió una reputación en la astronomía.
Arquímedes pudo haber estudiado en Alejandría durante algún tiempo con los estudiantes de Euclides , y se mantiene la comunicación con los matemáticos allí, como Conón , Dosite y Eratóstenes .
La leyenda cuenta que Siracusa resistió el asedio de Roma durante casi tres años, debido a las máquinas de guerra ingeniosos inventados por Arquímedes para dejar a sus enemigos en la distancia. Entre ellos: catapultas para lanzar piedras , cuerdas , poleas y ganchos para levantar y destruir las naves romanas ; inventos para quemar las naves.
Los trabajos de Arquímedes presenta una gran originalidad , habilidad computacional y la precisión en las declaraciones. Hay alrededor de diez tratados que se han conservado hasta nuestros días y hay rastros de otros.
Los tratados sobre geometría plana son: La medida de un círculo donde Arquímedes inauguró el clásico método para el cálculo de http://www.matematica.br/historia/imagens/arquimedes-001.jpg ; cuadratura de la parábola constituida veinticuatro proposiciones que muestra que el área de un segmento parabólico es de cuatro tercios del triángulo inscrito misma base y vértice en el punto en el que la tangente es paralela a la superficie de base . Esto implica la deducción de la suma de una serie geométrica convergente ; Sobre espirales compuestas veintiocho proposiciones que se dedican a las propiedades de la curva ( hoy conocido como Arquímedes espiral ) y cuya ecuación polar es http://www.matematica.br/ historia/imagens/arquimedes-002.jpg , en particular, es el área abarcada por los radios de curva y dos vectores de una manera sustancialmente la misma que la de un ejercicio ahora ser área de cálculo de la integral .
A través de los árabes saben que la fórmula habitual para el área de un triángulo en términos de sus lados , conocidos como la fórmula de Herón - donde s es el semiperímetro - era conocida por Arquímedes varios siglos antes del nacimiento de la garza . Pappus menciona en sus obras las palancas de Arquímedes tratado acerca de la CITES y Teon en sus puestos de trabajo por el teorema de Arquímedes encontró en el tratado La Teoría de los Espejos.
Los tratados sobre geometría espacial son: Sobre la esfera y el cilindro por escrito en dos volúmenes y se compone de cincuenta y tres proposiciones sobre , entre otras cosas , el teorema que proporciona áreas de una esfera y un casquete esférico . Muestra que el área de una superficie esférica es exactamente dos tercios de la superficie total del cilindro circular recto circunscritos a la misma y el volumen de la esfera es exactamente dos tercios del volumen del mismo cilindro . Libro II incluye el problema de cortar una esfera con un plan con el fin de obtener dos segmentos esféricos cuyos volúmenes se dan una razón. Este problema lleva a una ecuación cúbica , donde se hace una discusión sobre las condiciones en las que el cubo puede tener una raíz real positiva .
Arquímedes escribió pequeñas obras de aritmética , uno de ellos es El contador de arena, que es una curiosa pregunta : ¿cómo determinar la cantidad de granos de arena puede llenar una esfera de radio y el centro de la Tierra alcanza el Sol , es decir , la tamaño del universo . En esta obra encontramos comentarios relacionados con la astronomía , donde Arquímedes utilizó el modelo del universo de Aristarco de Samos , quien avanzó la teoría heliocéntrica de Copérnico . Arquímedes calculará la cantidad de arena necesaria para llenar un dedal , un estadio, el volumen de la Tierra y así sucesivamente, hasta que llena todo el universo. Simultáneamente y en paralelo , se desarrollará un sistema de numeración (que condujo a la invención de los logaritmos ) puede expresar los valores encontrados en este cálculo . También está el problema del ganado que implica ocho enteros siete incógnitas relacionadas con ecuaciones lineales y todavía sujeto a dos condiciones adicionales a saber, que la suma de incógnitas par derecho de un cuadrado perfecto y la suma de otro par se le da un número de incógnitas triangular . No hay condiciones adicionales , los menores valores de las incógnitas son números en los millones , con estas condiciones, una de las incógnitas que haber un número con más de 206 500 dígitos!
Hay dos trabajos de Arquímedes sobre las matemáticas aplicadas : Sobre el equilibrio de las figuras planas y Sobre los cuerpos flotantes . La primera de ellas se compone de dos libros y contiene veinticinco proposiciones que a través de un tratamiento postulacional , se obtienen las propiedades elementales de los centroides y el baricentro determinar diversas zonas planas , que termina con el segmento parabólico y un área limitada de una parábola y dos cadenas paralelas . Sobre los cuerpos flotantes se compone de dos libros noventa proposiciones , y representa la primera aplicación de las matemáticas a la hidrostática. El tratado se basa en dos postulados primero el desarrollo de las leyes familiares de la hidrostática y luego considera algunos problemas muy difíciles , para concluir con un notable estudio sobre la posición de reposo y la estabilidad de un (recto ) segmento de paraboloide de revolución sumergido en un fluido .
El tratado El método es en la forma de una carta dirigida a Eratóstenes y es importante debido a la información que proporciona en el método de Arquímedes utiliza para descubrir muchos de sus teoremas. Arquímedes utilizó experimentalmente para averiguar los resultados que luego trató de poner en términos rigurosos por el método de agotamiento.
Se le atribuyen otros dos puestos de trabajo perdidos Arquímedes : Acerca de Calendario y sobre la construcción de las bolas . En este último había una descripción de un planetario construido por él para mostrar los movimientos del Sol, la Luna y los cinco planetas conocidos en su época. Probablemente el mecanismo fue provocada por el agua.




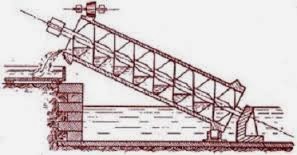
La invención mecánica más conocido de Arquímedes es el tornillo de la bomba de agua , construyó para irrigar los campos , estanques de drenaje y eliminan el agua de sentina de los barcos . El molino se sigue utilizando hoy en día en Egipto

Tweet