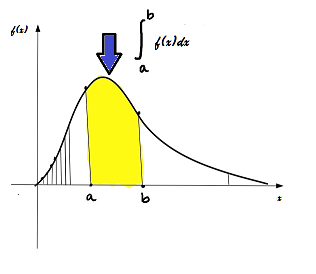
Desvendando os Segredos das Integrais
Todo o cálculo que aprendemos nos cursos de Matemática, se desenvolvem em torno da derivada e da integral. Enquanto que a derivada está ligada ao problema de traçar a tangente a uma curva, a integral está ligada ao problema de determinar a área de uma figura plana qualquer.
Todo o cálculo que aprendemos nos cursos de Matemática, se desenvolvem em torno da derivada e da integral. Enquanto que a derivada está ligada ao problema de traçar a tangente a uma curva, a integral está ligada ao problema de determinar a área de uma figura plana qualquer.
Na Geometria elementar vista no ensino fundamental, a área de um polígono qualquer é sempre introduzida em termos da área do triângulo, já que o polígono pode ser decomposto em triângulos. Mas, no caso de um círculo, a situação não é tão simples, sendo que para determinarmos sua área que é igual a π.R² temos que usar o limite também já visto por nós neste blog. Se quiser recordar, clique no post: Limites .
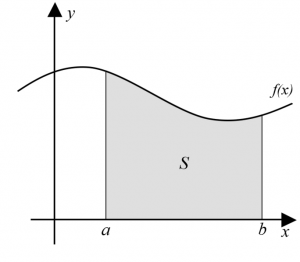
Agora, vamos dividir o intervalo [a,b] em n subintervalos iguais, de comprimento ▲x = (b-a) / n.
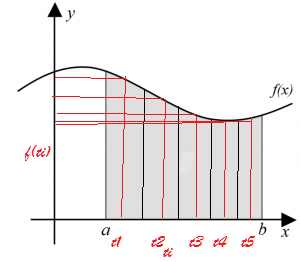
Sejam x0=a<x1<x2<...<xn=b, os pontos dessa divisão. Em cada um desses subintervalos, escolhemos pontos quaisquer: t1, t2, t3, ...,tn, sendo t1 no 1º intervalo, t2 no segundo, etc.
Dessa forma, formamos n retângulos, todos com base ▲x e alturas dadas por f(t1), f(t2),...,f(tn).
Veja no gráfico abaixo algumas divisões:
Sn= f(t1)▲x+f(t2)▲x+...+f(tn)▲x, ou por:
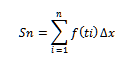
Vamos imaginar que essas somas sejam calculadas para todos os valores de n, de modo que obtemos toda uma sequência infinita de somas: S1, S2, S3, ..., Sn, ...
Isso nos faz pensar que esses valores de Sn se aproximam de valor limite, à medida que n cresce acima de qualquer número dado, o que nos sugere a definir como sendo a área da figura delimitada pelo gráfico de f(x), pelos eixos x e pelas retas: x= a e x=b. Essa área é chamada a integral de f(x) no intervalo [a,b] que podemos indicar por:
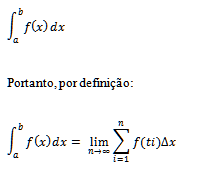
Observações muito importantes:
1. Quando existe o limite das somas Sn, dizemos que a função f(x) é integrável no intervalo [a,b].
2. A integral no intervalo [a,b] (lê-se integral de a até b), esses números a e b são chamados respectivamente os limites de integração inferior e superior e a função f é chamada integrando.
3. O símbolo de integral (∫) é devido ao Matemático Leibniz que o usou em seus trabalhos e representava uma soma na grafia antiga da letra S. Hoje ele representa o limite de uma sequência de somas.
4. f(x).dx seria no entender de Leibniz, a área de um retângulo infinitesimal de base infinitamente pequena dx e altura f(x). A integral de f, de a até b, seria então, a soma de todos esses retângulos infinitesimais.
5. Na igualdade verificada na definição de integral acima exposta, estamos supondo que a<b, no entanto de ocorrer o oposto temos que: ∫ f(x)dx, em [a,b] = -∫f(x)dx, em[b,a].
6. Caso ocorra integração no mesmo intervalo, por exemplo [a,a], sua integral será zero, ou seja:
∫f(x)dx em [a,a] =0
1) ∫ dx
Exercícios
Resolva usando as regras acima:
1) ∫ dx
∫ dx = x+c
2) ∫ x³.dx
∫ x³.dx = x^4 /4 +c
3) ∫ 3x^4.dx
∫3 x^4.dx =3∫x^4.dx = 3x^5 /5 +c
4) ∫ (4x^5+7).dx
∫ (4x^5+7).dx =∫ (4x^5).dx+ ∫ (7).dx
=4∫x^5.dx + 7∫dx = 4x^6 /6 + 7x +c (simplificando(÷2))→
=2x^6 /3 +7x +c
5) ∫ 5x^7.dx
∫5 x^7.dx =5∫x^7.dx = 5x^8 /8 +c
6) ∫ (5+3x²-7x³).dx
∫(5+3x²-7x³)dx = ∫5.dx+∫3x².dx-∫7x³.dx
=5∫dx+3∫x²dx-7∫x³dx = 5x +3x³/3 - 7x^4 /4 +c
=5x+x³-7x^4 /4 +c
Lembrete: a^(-p) = 1/ a^p
7) ∫ dx/x^4
∫dx/x^4 =∫x^-4.dx = x^-4+1 / -4+1 +c = x^-3 /-3 +c
=1/-3x^3 +c
8) ∫ x^3/2.dx
∫x^3/2 dx = x^3/2 +1 ÷ 3/2+1 +c
= x^5/2 ÷ 5/2 +c = 2/5 x^5/2 +c
 |
| A Matemática Aqui é Simples e Descomplicada! |
Você poderá gostar também de:
Limites
Derivada
Limites e Continuidade
Operações Fundamentais com Frações
Linkwithin
