Aprendizado
- Linus Pauling
Linus Pauling Linus Pauling (kanan) yang diberikan. Linus Carl Pauling adalah seorang ahli kimia Amerika yang mulia. Dilahirkan pada tahun 1901 dan meninggal dunia pada tahun 1994, dengan 93 tahun dedikasi untuk penyelidikan. Pauling adalah salah seorang...
- Thales Dari Miletus
InfoEscola : Melayari dan Pembelajaran Oleh Ana Lucia Santana Ini ahli falsafah pra -Socrates dianggap sebagai bapa falsafah Barat. Keturunan orang-orang Phoenicia , beliau dilahirkan di sebuah tanah jajahan purba Greece, Miletus , yang terletak di...
- Evangelista Torricelli
Evangelista Torricelli Dilahirkan pada tahun 1608 di Faenza , Itali, Evangelista Torricelli belajar di sebuah sekolah Jesuit. Pada sembilan belas beliau memasuki Universiti Rom, di mana beliau belajar matematik di bawah bimbingan Benedetto Castelli...
- Evangelista Torricelli
Evangelista Torricelli Dilahirkan pada tahun 1608 di Faenza , Itali, Evangelista Torricelli belajar di sebuah sekolah Jesuit. Pada sembilan belas beliau memasuki Universiti Rom, di mana beliau belajar matematik di bawah bimbingan Benedetto Castelli...
- René Descartes
René Descartes René Descartes , ahli falsafah dan ahli matematik , yang dilahirkan di La Haye, Touraine , kira-kira 300 kilometer di barat daya Paris pada 31 Mac, 1596. Bapanya, Joachim Descartes, peguam dan hakim , dimiliki tanah dan tajuk tuan...
Aprendizado
Archimedes
Archimedes

Tempoh : kira-kira 287-212 B.C.
Isu-isu matematik yang terlibat:
· Algebra : persamaan padu; sistem penomboran ; persamaan linear ;
· Fizikal: hidrostatik , pam air skru ;
· Spatial Geometri : bidang sfera , topi sfera , luas permukaan sfera , jumlah sfera ;
· Plane Geometri : Kaedah klasik untuk mengira pi , kuadratur parabola ; Archimedes Spiral ; formula Heron ;
Salah seorang ahli matematik terbesar abad ketiga SM, dari bandar Syracuse, di pulau Sicily. Dilahirkan kira-kira tahun 287 SM dan meninggal dunia semasa Perang Punic Kedua dalam 212 SM di Syracuse . Beliau adalah anak kepada ahli astronomi dan juga memperoleh reputasi dalam bidang astronomi .
Archimedes mungkin telah dipelajari di Alexandria untuk beberapa waktu dengan pelajar-pelajar Euclid , dan mengekalkan komunikasi dengan ahli matematik di sana, seperti Conon , Dosite dan Eratosthenes .
Lagenda mengatakan bahawa Syracuse menentang pengepungan Rom selama hampir tiga tahun , kerana mesin perang bijak dicipta oleh Archimedes untuk meninggalkan musuh anda di jarak yang jauh. Antaranya : tarbil untuk membuang batu-batu , tali, kapi dan cangkuk untuk mengangkat dan menghancurkan kapal-kapal Rom; ciptaan untuk membakar kapal-kapal.
Kerja-kerja Archimedes mempamerkan keaslian besar , kemahiran pengiraan dan ketepatan di dalam penyata . Terdapat kira-kira sepuluh perjanjian yang telah dipelihara hingga ke hari ini dan terdapat kesan lain.
Ini karya mengenai geometri satah ialah: Ukuran bulatan di mana Archimedes dirasmikan kaedah klasik untuk mengira http://www.matematica.br/historia/imagens/arquimedes-001.jpg ; Menyegiempatkan perumpamaan yang ditubuhkan dua puluh empat usul yang menunjukkan bahawa kawasan suatu segmen parabola adalah empat pertiga daripada asas segitiga tertulis sama dan bucu pada titik di mana tangen selari dengan bahagian dasar. Ini melibatkan ditolak jumlah satu siri geometri tumpu ; Mengenai pilin terdiri dua puluh lapan usul yang dikhaskan untuk sifat-sifat lengkung ( dikenali hari ini sebagai Archimedes Spiral ) dan yang kutub persamaan adalah http://www.matematica.br/ historia/imagens/arquimedes-002.jpg , khususnya, adalah kawasan yang termasuk dalam jejari lengkung dan dua vektor dengan cara yang ketara sama dengan latihan kini menjadi kawasan pengiraan penting.
Melalui orang-orang Arab tahu bahawa formula biasa untuk kawasan segi tiga dari segi penjurunya , yang dikenali sebagai formula Heron - di mana s adalah semiperímetro - telah diketahui Archimedes beberapa abad sebelum Heron dilahirkan. Pappus menyebut dalam karya-karya beliau tuil Archimedes perjanjian Mengenai memetik dan Teon dalam pekerjaan mereka teorem Archimedes mendapati dalam buku penerangan Teori Cermin .
Ini karya mengenai geometri ruang adalah: Pada Sfera dan Silinder ditulis dalam dua jilid dan terdiri lima puluh tiga usul tentang, antara lain, teorem yang menyediakan bidang sfera dan topi bulat. Menunjukkan bahawa luas permukaan sfera betul-betul dua pertiga daripada jumlah luas permukaan silinder bulat yang betul terbatas kepadanya dan jumlah sfera ini betul-betul dua pertiga daripada jumlah silinder yang sama. Buku II merangkumi masalah penghirisan sfera dengan rancangan untuk mendapatkan dua segmen sfera yang jilid diberi sebab. Masalah ini membawa kepada persamaan padu di mana perbincangan yang dibuat mengenai keadaan di mana kiub boleh mempunyai punca nyata yang positif.
Archimedes menulis karya kecil di aritmetik, salah seorang daripada mereka adalah Kaunter pasir, yang merupakan soalan ingin tahu : bagaimana untuk menentukan jumlah butiran pasir boleh mengisi sfera berjejari dan pusat di Bumi mencapai Matahari, iaitu, saiz alam semesta. Dalam karya ini kita dapati komen yang berkaitan dengan astronomi , di mana Archimedes menggunakan model alam semesta Aristarchus dari Samos, yang mara teori heliosentrik Copernicus . Archimedes akan mengira jumlah pasir yang diperlukan untuk mengisi bidal , stadium , jumlah bumi dan sebagainya, sehingga ia mengisi seluruh alam semesta. Pada masa yang sama dan selari , akan membangunkan sistem penomboran (yang membawa kepada penciptaan logaritma ) boleh meluahkan nilai-nilai yang terdapat dalam pengiraan ini. Terdapat juga masalah lembu yang melibatkan lapan keseluruhan tujuh diketahui berkaitan persamaan linear dan masih tertakluk kepada dua syarat tambahan iaitu jumlah tidak diketahui pasangan hak kuasa dua sempurna dan jumlah pasangan lain diberikan pelbagai ketidakpastian segi tiga. Tiada syarat-syarat tambahan , nilai paling rendah yang tidak diketahui nombor dalam berjuta-juta , dengan syarat-syarat ini , salah satu yang tidak diketahui mestilah nombor dengan lebih daripada 206 500 digit !
Terdapat dua karya Archimedes pada matematik gunaan : Pada Keseimbangan Angka Pesawat dan Mayat Terapung . Yang pertama terdiri daripada dua buah buku dan mengandungi dua puluh lima usul yang melalui rawatan postulacional , kita mendapatkan sifat-sifat rendah daripada sentroid dan sentroid menentukan pelbagai kawasan rata , yang berakhir dengan segmen parabola dan kawasan yang terhad parabola dan dua tali selari. Mayat Terapung terdiri daripada dua buah buku sembilan puluh usul, dan mewakili permohonan pertama matematik untuk hidrostatik. Perjanjian itu adalah berdasarkan dua postulat pertama membangunkan undang-undang biasa hidrostatik dan kemudian menganggap beberapa masalah yang sangat sukar , dan menyimpulkan dengan kajian perlu diberi perhatian pada kedudukan berehat dan kestabilan ( lurus) segmen paraboloid revolusi direndam di dalam bendalir .
Karya Kaedah adalah dalam bentuk surat kepada Eratosthenes dan adalah penting kerana maklumat yang ia menyediakan kaedah yang Archimedes digunakan untuk menemui banyak teorem beliau. Archimedes digunakan uji kaji untuk mengetahui keputusan bahawa dia kemudian cuba untuk meletakkan dari segi ketat oleh kaedah menyeluruh .
Adalah disebabkan oleh dua pekerjaan lain hilang Archimedes : Mengenai Kalendar dan Mengenai Membina bola. Dalam kedua terdapat penerangan planetarium yang dibina olehnya untuk menunjukkan pergerakan matahari, bulan dan lima planet dikenali pada zamannya. Mungkin mekanisme itu dicetuskan oleh air.
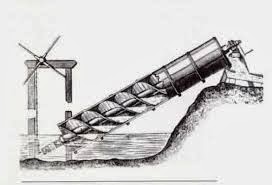
Penciptaan terkenal mekanikal Archimedes adalah skru pam air , beliau membina untuk mengairi sawah , kolam longkang dan membuang air lambung kapal dari kapal-kapal . Kilang ini masih digunakan hari ini di Mesir

Tempoh : kira-kira 287-212 B.C.
Isu-isu matematik yang terlibat:
· Algebra : persamaan padu; sistem penomboran ; persamaan linear ;
· Fizikal: hidrostatik , pam air skru ;
· Spatial Geometri : bidang sfera , topi sfera , luas permukaan sfera , jumlah sfera ;
· Plane Geometri : Kaedah klasik untuk mengira pi , kuadratur parabola ; Archimedes Spiral ; formula Heron ;
Salah seorang ahli matematik terbesar abad ketiga SM, dari bandar Syracuse, di pulau Sicily. Dilahirkan kira-kira tahun 287 SM dan meninggal dunia semasa Perang Punic Kedua dalam 212 SM di Syracuse . Beliau adalah anak kepada ahli astronomi dan juga memperoleh reputasi dalam bidang astronomi .
Archimedes mungkin telah dipelajari di Alexandria untuk beberapa waktu dengan pelajar-pelajar Euclid , dan mengekalkan komunikasi dengan ahli matematik di sana, seperti Conon , Dosite dan Eratosthenes .
Lagenda mengatakan bahawa Syracuse menentang pengepungan Rom selama hampir tiga tahun , kerana mesin perang bijak dicipta oleh Archimedes untuk meninggalkan musuh anda di jarak yang jauh. Antaranya : tarbil untuk membuang batu-batu , tali, kapi dan cangkuk untuk mengangkat dan menghancurkan kapal-kapal Rom; ciptaan untuk membakar kapal-kapal.
Kerja-kerja Archimedes mempamerkan keaslian besar , kemahiran pengiraan dan ketepatan di dalam penyata . Terdapat kira-kira sepuluh perjanjian yang telah dipelihara hingga ke hari ini dan terdapat kesan lain.
Ini karya mengenai geometri satah ialah: Ukuran bulatan di mana Archimedes dirasmikan kaedah klasik untuk mengira http://www.matematica.br/historia/imagens/arquimedes-001.jpg ; Menyegiempatkan perumpamaan yang ditubuhkan dua puluh empat usul yang menunjukkan bahawa kawasan suatu segmen parabola adalah empat pertiga daripada asas segitiga tertulis sama dan bucu pada titik di mana tangen selari dengan bahagian dasar. Ini melibatkan ditolak jumlah satu siri geometri tumpu ; Mengenai pilin terdiri dua puluh lapan usul yang dikhaskan untuk sifat-sifat lengkung ( dikenali hari ini sebagai Archimedes Spiral ) dan yang kutub persamaan adalah http://www.matematica.br/ historia/imagens/arquimedes-002.jpg , khususnya, adalah kawasan yang termasuk dalam jejari lengkung dan dua vektor dengan cara yang ketara sama dengan latihan kini menjadi kawasan pengiraan penting.
Melalui orang-orang Arab tahu bahawa formula biasa untuk kawasan segi tiga dari segi penjurunya , yang dikenali sebagai formula Heron - di mana s adalah semiperímetro - telah diketahui Archimedes beberapa abad sebelum Heron dilahirkan. Pappus menyebut dalam karya-karya beliau tuil Archimedes perjanjian Mengenai memetik dan Teon dalam pekerjaan mereka teorem Archimedes mendapati dalam buku penerangan Teori Cermin .
Ini karya mengenai geometri ruang adalah: Pada Sfera dan Silinder ditulis dalam dua jilid dan terdiri lima puluh tiga usul tentang, antara lain, teorem yang menyediakan bidang sfera dan topi bulat. Menunjukkan bahawa luas permukaan sfera betul-betul dua pertiga daripada jumlah luas permukaan silinder bulat yang betul terbatas kepadanya dan jumlah sfera ini betul-betul dua pertiga daripada jumlah silinder yang sama. Buku II merangkumi masalah penghirisan sfera dengan rancangan untuk mendapatkan dua segmen sfera yang jilid diberi sebab. Masalah ini membawa kepada persamaan padu di mana perbincangan yang dibuat mengenai keadaan di mana kiub boleh mempunyai punca nyata yang positif.
Archimedes menulis karya kecil di aritmetik, salah seorang daripada mereka adalah Kaunter pasir, yang merupakan soalan ingin tahu : bagaimana untuk menentukan jumlah butiran pasir boleh mengisi sfera berjejari dan pusat di Bumi mencapai Matahari, iaitu, saiz alam semesta. Dalam karya ini kita dapati komen yang berkaitan dengan astronomi , di mana Archimedes menggunakan model alam semesta Aristarchus dari Samos, yang mara teori heliosentrik Copernicus . Archimedes akan mengira jumlah pasir yang diperlukan untuk mengisi bidal , stadium , jumlah bumi dan sebagainya, sehingga ia mengisi seluruh alam semesta. Pada masa yang sama dan selari , akan membangunkan sistem penomboran (yang membawa kepada penciptaan logaritma ) boleh meluahkan nilai-nilai yang terdapat dalam pengiraan ini. Terdapat juga masalah lembu yang melibatkan lapan keseluruhan tujuh diketahui berkaitan persamaan linear dan masih tertakluk kepada dua syarat tambahan iaitu jumlah tidak diketahui pasangan hak kuasa dua sempurna dan jumlah pasangan lain diberikan pelbagai ketidakpastian segi tiga. Tiada syarat-syarat tambahan , nilai paling rendah yang tidak diketahui nombor dalam berjuta-juta , dengan syarat-syarat ini , salah satu yang tidak diketahui mestilah nombor dengan lebih daripada 206 500 digit !
Terdapat dua karya Archimedes pada matematik gunaan : Pada Keseimbangan Angka Pesawat dan Mayat Terapung . Yang pertama terdiri daripada dua buah buku dan mengandungi dua puluh lima usul yang melalui rawatan postulacional , kita mendapatkan sifat-sifat rendah daripada sentroid dan sentroid menentukan pelbagai kawasan rata , yang berakhir dengan segmen parabola dan kawasan yang terhad parabola dan dua tali selari. Mayat Terapung terdiri daripada dua buah buku sembilan puluh usul, dan mewakili permohonan pertama matematik untuk hidrostatik. Perjanjian itu adalah berdasarkan dua postulat pertama membangunkan undang-undang biasa hidrostatik dan kemudian menganggap beberapa masalah yang sangat sukar , dan menyimpulkan dengan kajian perlu diberi perhatian pada kedudukan berehat dan kestabilan ( lurus) segmen paraboloid revolusi direndam di dalam bendalir .
Karya Kaedah adalah dalam bentuk surat kepada Eratosthenes dan adalah penting kerana maklumat yang ia menyediakan kaedah yang Archimedes digunakan untuk menemui banyak teorem beliau. Archimedes digunakan uji kaji untuk mengetahui keputusan bahawa dia kemudian cuba untuk meletakkan dari segi ketat oleh kaedah menyeluruh .
Adalah disebabkan oleh dua pekerjaan lain hilang Archimedes : Mengenai Kalendar dan Mengenai Membina bola. Dalam kedua terdapat penerangan planetarium yang dibina olehnya untuk menunjukkan pergerakan matahari, bulan dan lima planet dikenali pada zamannya. Mungkin mekanisme itu dicetuskan oleh air.

Penciptaan terkenal mekanikal Archimedes adalah skru pam air , beliau membina untuk mengairi sawah , kolam longkang dan membuang air lambung kapal dari kapal-kapal . Kilang ini masih digunakan hari ini di Mesir
loading...
- Linus Pauling
Linus Pauling Linus Pauling (kanan) yang diberikan. Linus Carl Pauling adalah seorang ahli kimia Amerika yang mulia. Dilahirkan pada tahun 1901 dan meninggal dunia pada tahun 1994, dengan 93 tahun dedikasi untuk penyelidikan. Pauling adalah salah seorang...
- Thales Dari Miletus
InfoEscola : Melayari dan Pembelajaran Oleh Ana Lucia Santana Ini ahli falsafah pra -Socrates dianggap sebagai bapa falsafah Barat. Keturunan orang-orang Phoenicia , beliau dilahirkan di sebuah tanah jajahan purba Greece, Miletus , yang terletak di...
- Evangelista Torricelli
Evangelista Torricelli Dilahirkan pada tahun 1608 di Faenza , Itali, Evangelista Torricelli belajar di sebuah sekolah Jesuit. Pada sembilan belas beliau memasuki Universiti Rom, di mana beliau belajar matematik di bawah bimbingan Benedetto Castelli...
- Evangelista Torricelli
Evangelista Torricelli Dilahirkan pada tahun 1608 di Faenza , Itali, Evangelista Torricelli belajar di sebuah sekolah Jesuit. Pada sembilan belas beliau memasuki Universiti Rom, di mana beliau belajar matematik di bawah bimbingan Benedetto Castelli...
- René Descartes
René Descartes René Descartes , ahli falsafah dan ahli matematik , yang dilahirkan di La Haye, Touraine , kira-kira 300 kilometer di barat daya Paris pada 31 Mac, 1596. Bapanya, Joachim Descartes, peguam dan hakim , dimiliki tanah dan tajuk tuan...
